문제
출처: https://www.acmicpc.net/problem/2873


처음 생각한 접근법
R행 C열 크기의 직사각형을 모눈종이에 그려보고 최대한 많은 경로를 이동하는 방법을 생각했습니다.
여러가지 경우의 수를 생각하다 보니 몇 가지 패턴이 보였습니다.
먼저 R 또는 C 가 홀수일 경우 모든 경로를 탐색 할 수 있었습니다. 즉 기쁨의 숫자와 상관 없이 R, L, U, D 를 조합하면 되었습니다.
- R이 홀수인 경우는 다음과 같은 패턴으로 이동합니다.

- C이 홀수인 경우 다음과 같은 패턴으로 이동합니다.

마지막으로 R과 C가 모두 짝수인 경우는 1칸만 방문 못하고 모든 곳을 방문한다고 생각했습니다. 하지만 여기서부터 잘못 생각하여 시간이 많이 뺏겼고 답을 도출해내지 못했습니다.
다음은 제가 생각한 경우의 수 입니다.

저는 처음에 경우의 수를 위 그림과 같이 2가지만 생각했습니다. 도착점([R-1][c-1])의 위나 왼쪽만 고려하여 둘 중 큰 값을 가진 곳으로 방문하면 된다고 생각했습니다.
그리고 위를 바탕으로 코드를 다음과 같이 작성하여 제출하였습니다.
처음 제출한 코드
import sys
R, C = map(int, sys.stdin.readline().split())
Graph = [list(map(int, sys.stdin.readline().split())) for _ in range(R)]
result = ''
# 행이 홀수일 경우
if R%2 == 1:
for i in range(R):
#홀수 번째 행
if i % 2 == 0:
result += 'R'*(C-1)
if i == R-1:
break
#짝수 번째 행
else:
result += 'L'*(C-1)
result += 'D'
#열이 홀수인 경우
elif C%2 == 1:
for i in range(C):
#홀수 번째 열
if i % 2 == 0:
result += 'D'*(R-1)
if i == C-1:
break
#짝수 번째 열
else:
result += 'U'*(R-1)
result += 'R'
#행, 열 모두 짝수인 경우 => 도착점 왼쪽, 위 중 큰 값으로 가면 됨
else:
# 왼쪽이 큰 경우
if Graph[R-1][C-2] >= Graph[R-2][C-1]:
for i in range(R-1):
# 아래에서 2번째 행일때
if i == R-2:
result += 'DR' + 'URDR' * int((C-2)/2)
# 홀수 번째 행
elif i % 2 == 0:
result += 'R' * (C - 1) + 'D'
# 짝수 번째 행
else:
result += 'L' * (C - 1) + 'D'
# 위쪽이 큰 경우
else:
for i in range(C-1):
# 아래에서 2번째 행일때
if i == C - 2:
result += 'RD' + 'LDRD' * int((R - 2) / 2)
# 홀수 번째 행
elif i % 2 == 0:
result += 'D' * (R - 1) + 'R'
# 짝수 번째 행
else:
result += 'U' * (R - 1) + 'R'
print(result)
오답 분석
7%는 맞았다고 나왔다가 틀렸습니다가 출력되는 것을 보고 짝수의 경우의 수를 더 생각해봤습니다. 그 결과 다음과 같은 경우의 수도 존재한다는 것을 깨달았습니다.
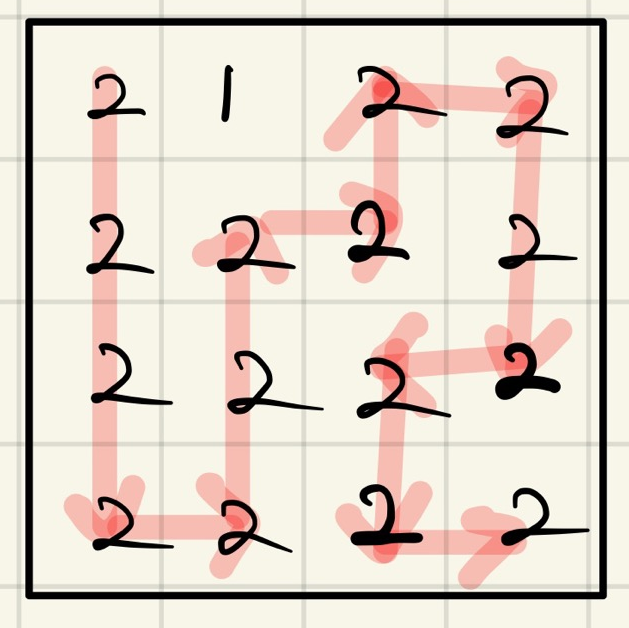
이렇게 여러가지 경우의 수가 더 존재하다는 것을 깨닫고 하루종일 고민을 하다가 도저히 풀리지 않아 구글링을 통해 힌트를 얻었습니다.
저는 한 블로그만 보면 객관적이거나 다양한 풀이 방법을 배우지 못한다고 생각해서 여러가지 사이트를 봤습니다. 하지만 대부분 체스판으로 설명을 하며 저와 비슷한 어려움을 겪은 분들이 생각보다 많았습니다.
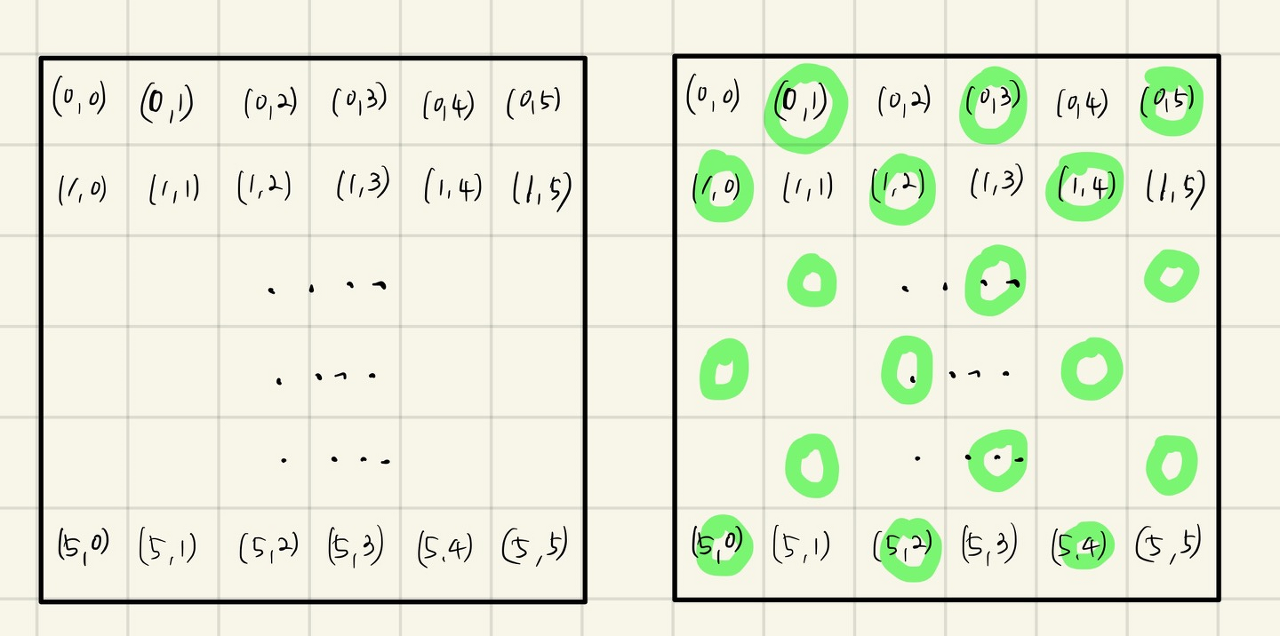
위 문제는 초록색으로 표시된 위치에서 최소값을 찾아 그 위치를 제외하고 지나가야 합니다. 여기서의 중요한 포인트는 초록색으로 표시된 위치의 패턴을 찾아야합니다.
여러가지로 패턴을 표현할 수 있지만 저는 이런경우에 수학적으로 접근하려고 합니다. R과 C를 그래프로 나타내었을 때 인덱스로 나타낸 x,y 좌표 값의 합이 홀수인 것을 파악하고 2중 for문을 돌려 최소값을 찾아내었습니다.
그런데 저는
‘만약 초록색으로 표시된 위치 말고 다른 위치에 최소값이 있으면 어떡하지?, 이것도 처리해줘야 하는 것 아닌가?’
하는 의문이 들었습니다.
하지만 여러가지 경우의 수를 체크해본 결과 이는 고려할 필요가 없는 경우였습니다.
그 이유는 만약 초록색으로 표시된 위치를 제외한 곳에 최소값이 있어 그 경우를 피하기 위해서는 초록색으로 표시된 위치 2개를 방문할 수 없게 됩니다.
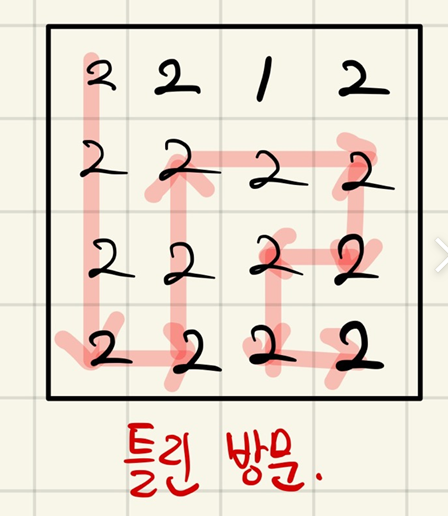
위 경우는 1이라는 최소값을 피하기 위해 임의의 방문 경로를 나타낸 것입니다. 하지만 그 1을 피하기 위해 양 옆 2군데를 모두 방문할 수 없게 됩니다.
즉 초록색으로 표시된 위치를 제외한 곳을 고려한 순간 그리디 알고리즘에서 벗어나게 되며 초록색으로 표시된 위치만을 고려했을 경우보다 무조건 기쁨의 합이 적게됩니다.
저는 이러한 경우의 수를 다 고려하여 다시 자세하게 경우의 수를 고려했습니다.
짝수 x 짝수 크기의 직사각형 경우의 수
위 문제는 행을 두 개씩 짝을 지어 풀어야 합니다. 그래야 지그재그 패턴이 아닌 다른 경로들을 바로 찾을 수 있기 때문이고 이게 곧 그리디 알고리즘이기 때문입니다.
저는 예시를 6 x 6 직사각형으로 하였지만 2, 4, 8, 10 등 모두 가능합니다.
1. 0~1 구간에 최소값이 존재하는 경우
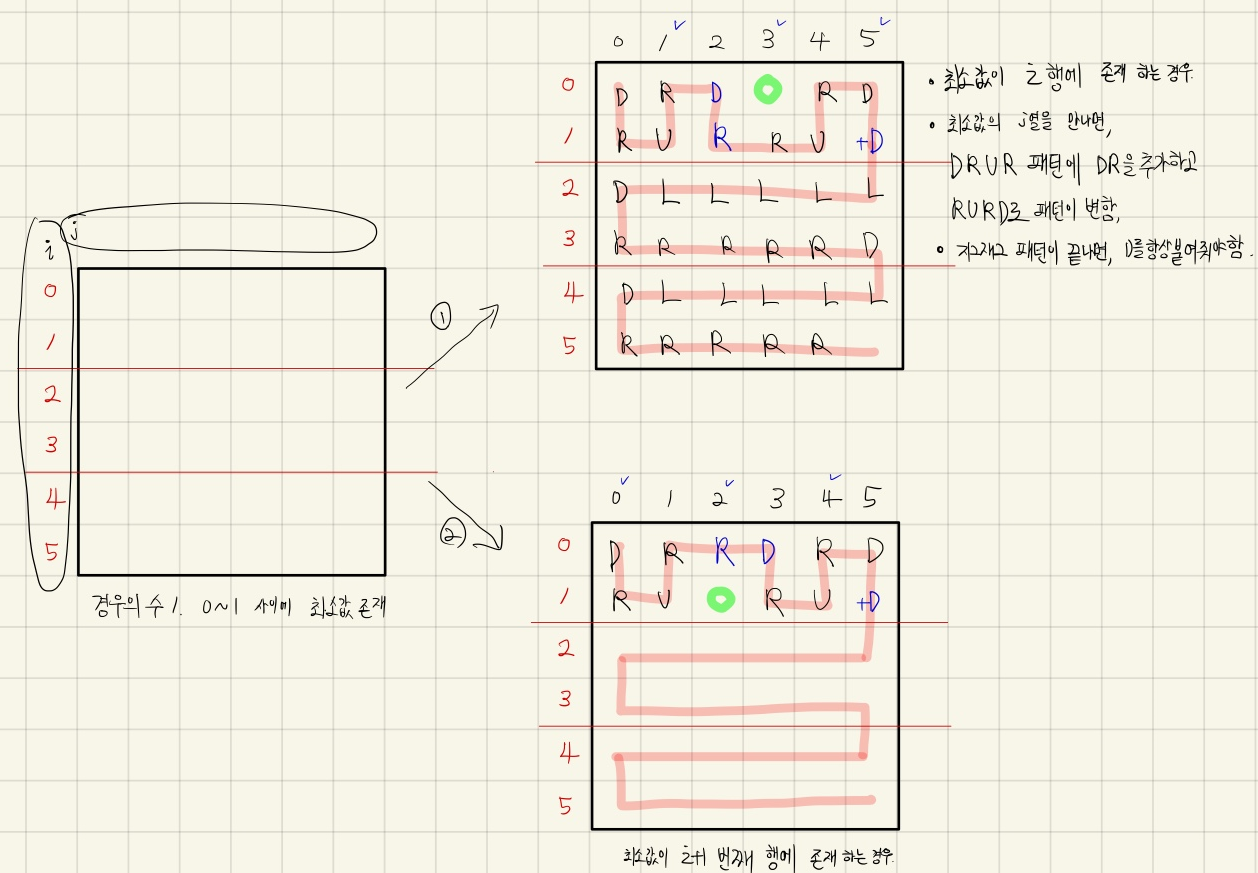
위 경우에서 최소값이 첫 번째 행 또는 두 번째 행에 존재하는 경우입니다.
처음부터 DRUR 패턴으로 for문을 1부터 시작하여 2씩 증가시킵니다. 만약 for문의 변수가 최소값의 열과 같아지는 경우가 생기면 DR을 추가하고 다음 반복문 부터는 RURD 패턴으로 변경하여 문자열을 저장합니다.
만약 최소값이 2개로 나눈 구간중 2번째에 나타난다면 DRUR 패턴을 반복하다가 RD를 결과에 저장하고 다음 반복 부터는 RURD를 추가합니다.
즉 최소값이 있는 칸을 방문하기 전까지는 DRUR 패턴과 방문하고 난 후 RURD 패턴은 같지만 위냐 아래냐에 따라 이동경로가 달라지는 경우를 구분지어야 합니다.
0~1구간이 종료되면 결과에 D 입력을 저장합니다. 다음 2개 행에 방문하기 전이 기 때문입니다.
코드는 다음과 같습니다.
저는 최소값을 지나는 경우를 PASS 라는 변수를 선언하여 구분지었습니다.
# MIN의 행 인덱스가 i 또는 i+1 일 경우
if MIN[1] == i:
for j in range(1, C, 2):
# 행 인덱스가 짝수일 경우
if MIN[2] == j:
result += 'DR'
PASS = True
else:
if PASS == False:
result += 'DRUR'
else:
result += 'RURD'
result += 'D'
elif MIN[1] == i + 1:
for j in range(0, C, 2):
# 행 인덱스가 홀수일 경우
if MIN[2] == j:
result += 'RD'
PASS = True
else:
if PASS == False:
result += 'DRUR'
else:
result += 'RURD'
result += 'D'2. 2~3 구간에 최소값이 존재하는 경우
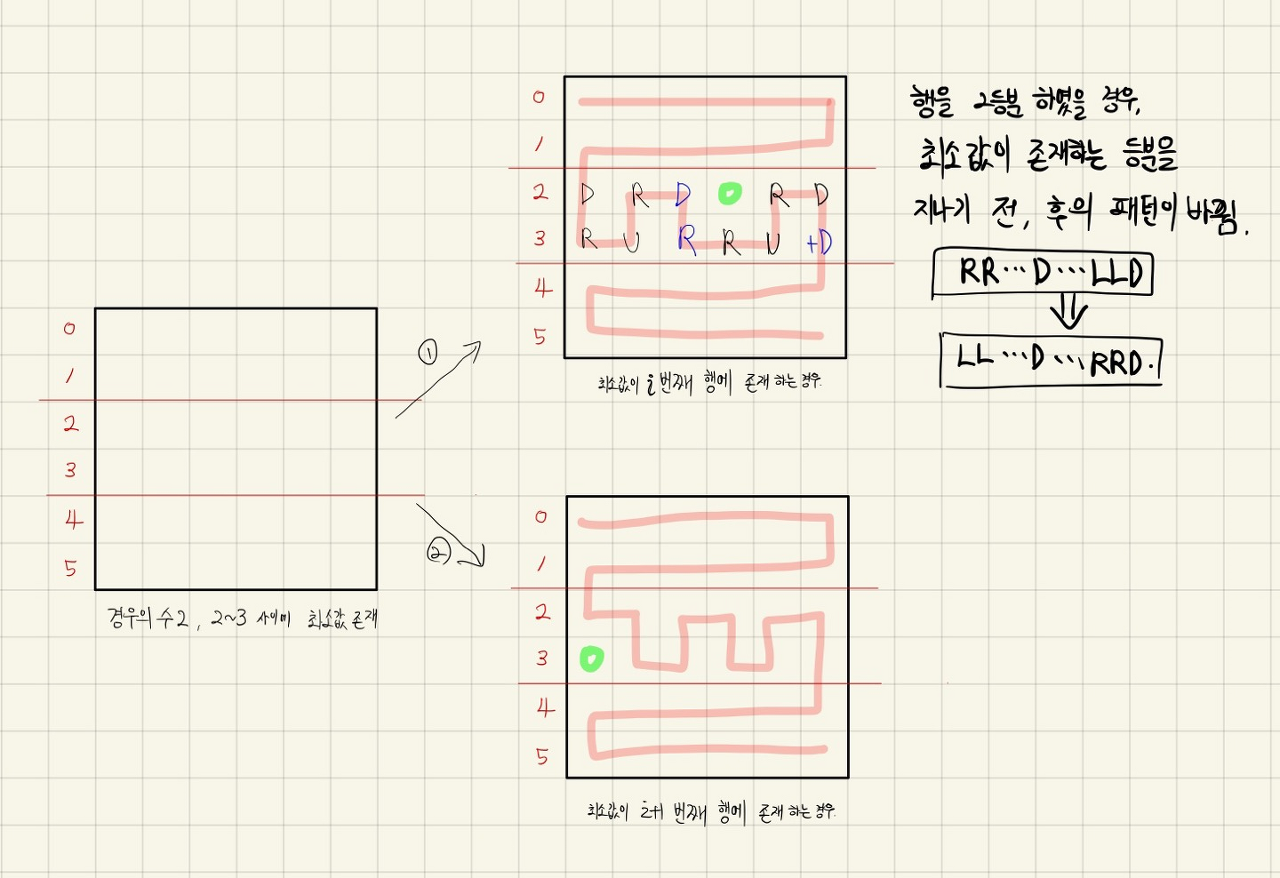
위 경우는 최소값이 중간에 존재하는 경우입니다. 위 예시는 6행 기준이고 일반적으론 [0,1], [n-2,n-1] 행을 제외한 모든 구간에서 적용이 가능합니다.
위 그림에서 보다 시피 중간 구간 이전과 이후의 패턴이 변화된 것을 볼 수 있습니다.
따라서 PASS가 True로 변하고 True 이후 부터는 패턴을 다르게 적용시켰습니다. 코드는 다음과 같습니다.
# 최솟값 안 지나고 MIN 행 인덱스가 i도 아니고 i+1 아닌 경우 ㄷ 반대 모양 만들기
else:
result += 'R' * (C-1) + 'D' + 'L' *(C-1) +'D'
else:
result += 'L' * (C - 1) + 'D' + 'R' * (C - 1) + 'D'정답 코드
import sys
R, C = map(int, sys.stdin.readline().split())
Graph = [list(map(int, sys.stdin.readline().split())) for _ in range(R)]
result = ''
# 행이 홀수일 경우
if R%2 == 1:
for i in range(R):
#홀수 번째 행
if i % 2 == 0:
result += 'R'*(C-1)
if i == R-1:
break
#짝수 번째 행
else:
result += 'L'*(C-1)
result += 'D'
print(result)
#열이 홀수인 경우
elif C%2 == 1:
for i in range(C):
#홀수 번째 열
if i % 2 == 0:
result += 'D'*(R-1)
if i == C-1:
break
#짝수 번째 열
else:
result += 'U'*(R-1)
result += 'R'
print(result)
#행, 열 모두 짝수인 경우 => x좌표,y좌표 인덱스 합이 홀수 중에서 가장 작은거 찾기
else:
MIN = [1001, 0, 1] # 최소값, x좌표, y좌표
PASS = False # 최소 지점을 지나간 경우를 표시
for i in range(R):
for j in range(C):
if (i+j)%2 == 1:
if MIN[0] > Graph[i][j]:
MIN = [Graph[i][j], i, j]
#print(MIN)
for i in range(0, R, 2):
if PASS == False:
# MIN의 행 인덱스가 i 또는 i+1 일 경우
if MIN[1] == i:
for j in range(1, C, 2):
# 행 인덱스가 짝수일 경우
if MIN[2] == j:
result += 'DR'
PASS = True
else:
if PASS == False:
result += 'DRUR'
else:
result += 'RURD'
result += 'D'
elif MIN[1] == i + 1:
for j in range(0, C, 2):
# 행 인덱스가 홀수일 경우
if MIN[2] == j:
result += 'RD'
PASS = True
else:
if PASS == False:
result += 'DRUR'
else:
result += 'RURD'
result += 'D'
# 최솟값 안 지나고 MIN 행 인덱스가 i도 아니고 i+1 아닌 경우 ㄷ 반대 모양 만들기
else:
result += 'R' * (C-1) + 'D' + 'L' *(C-1) +'D'
else:
result += 'L' * (C - 1) + 'D' + 'R' * (C - 1) + 'D'
print(result[0:-1])#마지막 D 는 뺌
후기
이 문제를 처음 제출한 건 22년 3월 1일 새벽 3시 였습니다. 이 문제를 거의 하루종일 매달리고 있었습니다. 즉 시작은 22년 2월 말이었습니다.
처음에 문제를 보았을 때, 그리디 유형이라서 문제가 단순하게 읽혀서 쉽게 생각했습니다. 정말 큰 오산이었습니다. 이 문제 때문에 3일동안 다른 백준 문제를 풀지 못했습니다. 그만큼 풀고 싶었고 포기하고 싶지 않았습니다.
그런데 도저히 짝수 x 짝수 크기의 정사각형 부지에서는 풀리지 않아 웹 검색을 해보았습니다. 단, 코드는 절대 보지 않았으며 아이디어만 얻었습니다.
모두 똑같이 체스판을 이용해서 설명을 하는 것을 보고 이 문제는 다른 아이디어를 생각하기 어려울 정도로 고난이도 문제라는 것을 깨달았으며, 아이디어나 접근법은 알아도 실제 많은 조건을 구분해 가며 구현해야 하기 때문에 실제로 매우 까다로웠습니다.
많이 어려웠지만 제가 정답을 맞아서 많이 높아봐야 골드1 이나 골드2 문제인 줄 알았는데 플레티넘 3라서 기분이 좋았고 그 동안의 스트레스랑 고통이 다 날라갔습니다.
비록 처음부터 끝까지 제 스스로 코드를 짜진 않았지만 홀수의 경우는 다 맞았고 짝수 부분도 힌트만 얻고 바로 코드로 구현해서 정답이 되었다는 것이 신기헀습니다.
이번을 계기로 더 열심히해서 다음에는 플레티넘 문제도 스스로 맞춰보도록 제 스스로를 단련시키겠습니다.
글을 다 쓰니 벌써 새벽 4시가 되었네요.. 얼른 자고 내일은 DFS/BFS 문제 풀어보도록 하겠습니다!
오타나 궁금한 점 있으면 github로 로그인 후 아래에 댓글 달아주세요! 질문과 피드백은 언제든지 환영입니다.
'ProblemSolving > 구현, 시뮬레이션, 완전탐색' 카테고리의 다른 글
| 백준 5373 큐빙 -(Python) (0) | 2022.04.03 |
|---|---|
| 백준 15685 드래곤 커브 - (Python) (0) | 2022.04.01 |
| 백준 14891 톱니바퀴 (Python) (0) | 2022.03.30 |
| 백준 14890 경사로 (Python) (0) | 2022.03.30 |
| 백준 14503 로봇 청소기 (python) (0) | 2022.03.29 |