문제
출처: https://www.acmicpc.net/problem/17779



나의 접근법
처음에는 마름모를 기준으로 위, 오른쪽, 아래, 왼쪽을 맵 경계까지 1부터 4를 차례로 넣고 BFS로 graph의 꼭지점을 시작으로 탐색하려고 했으나 경계의 네 변의 길이가 모두 같은 경우는 쉽지만 마름모의 두 쌍의 길이가 다를 때는 범위 파악이 힘들었고 이렇게 해도 경계는 그려야 하기 때문에 BFS를 하지 않고 바로 반복문을 돌렸습니다.
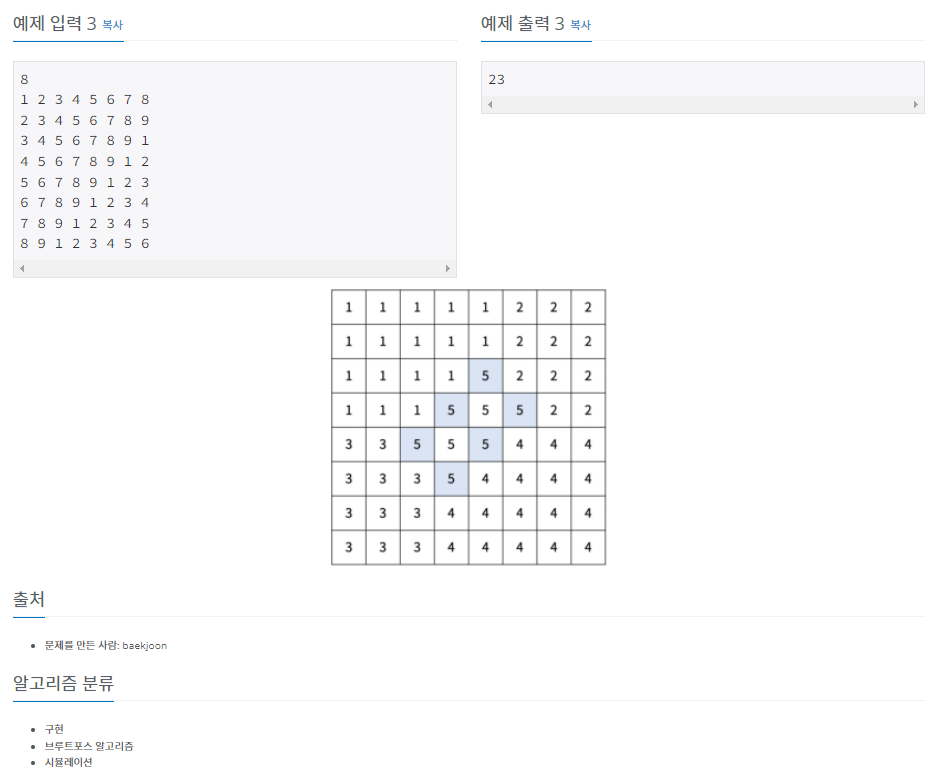
구간을 5개로 나누는데 경계선 내부인 5번 선거구는 값을 넣지 않습니다.
구간을 나누는 방법은 x, y를 한 쌍을 기준으로 잡아 4부분으로 나누어 for문을 돌려 경계를 나누었습니다.
그리고 예를 들어 4번 지역은 행이 감소하면서 열이 증가하는 순서로 탐색하면 자칫 탐색을 못하는 경우가 생겼는데 이러한 버그를 찾기 위해 그래프에 구역별로 1~4까지 값을 넣어가며 구현했습니다.
5번 선거구에 있는 인구 수는 미리 전체 인구수를 구하고 1~4 선거구의 인구수를 모두 더해 빼주는 식으로 찾았습니다.
정답 코드
def boundary(x, y, d1, d2, tempGraph):
for i in range(d1):
tempGraph[x + i][y - i] = 5
for i in range(1, d2+1):
tempGraph[x + i][y + i] = 5
for i in range(d2+1):
tempGraph[x + d1 + i][y - d1 + i] = 5
for i in range(1, d1+1):
tempGraph[x + d2 + i][y + d2 - i] = 5
return tempGraph
N = int(input())
total1to4 = 0
graph = [[0 for _ in range(N+1)]]
for i in range(1, N+1):
data = [0] + (list(map(int, input().split())))
total1to4 += sum(data)
graph.append(data)
ans = int(10e9)
temp = []
for x in range(1, N):
for y in range(1, N):
for d1 in range(1, N+1):
for d2 in range(1, N+1):
tempGraph = [[0]*(N+1) for i in range(N+1)]
result = [0,0,0,0,0]
if x < x+d1+d2 <= N and 1 <= y-d1 < y < y+d2 <= N:
tempGraph = boundary(x, y, d1, d2, tempGraph)
# 1번 선거구
for i in range(1, x+d1):
for j in range(1, y+1):
if tempGraph[i][j] == 5:
break
result[0] += graph[i][j]
tempGraph[i][j] = 1
# 2번 선거구
for i in range(1, x+d2+1):
#for j in range(y+1, N+1):
for j in range(N, y, -1):
if tempGraph[i][j] == 5:
break
result[1] += graph[i][j]
tempGraph[i][j] = 2
# 3번 선거구
for i in range(x + d1, N+1):
for j in range(1, y-d1+d2):
if tempGraph[i][j] == 5:
break
result[2] += graph[i][j]
tempGraph[i][j] = 3
# 4번 선거구
for i in range(x+d2+1, N+1):
#for j in range(N, y + d2 - d1 -1, -1):
for j in range(N, y-d1+d2-1, -1):
if tempGraph[i][j] == 5:
break
result[3] += graph[i][j]
tempGraph[i][j] = 4
#5번 선거구 세기
result[4] = total1to4 - sum(result)
ans = min(ans, (max(result) - min(result)))
temp.append(ans)
print(ans)후기
처음부터 범위 나누는 방법이 잘 이해가 되지 않아 여러 번 보았던 문제였습니다. 결국 d1은 마름모로 생각했을 때 왼쪽 아래로 내려가는 대각선이고 d2는 오른쪽으로 내려가는 대각선을 나타낸 것을 알아냈습니다.
하지만 문제를 볼 수록 제가 풀면 하루는 넘길 것 같았습니다. 저는 특히 경계 구하는 것을 까다롭고 어려워했었는데 위 문제를 풀면서 경계구하는 것을 극악 난이도라고 생각하여 빠르게 검색을 하며 이해하기로 했습니다.
인덱스 기준이 아닌 1행 1열 기준으로 시작하는 그래프라면 그래프에 값을 받기 전에 1행과 1열에 0을 다음과 같이 미리 넣어 계산하는 것이 복잡성을 줄여주었습니다.
graph = [[0 for _ in range(N+1)]]
for i in range(1, N+1):
data = [0] + (list(map(int, input().split())))
경계는 위 문제에서 주어진 대로 붙여넣기만 하면 되어 오히려 친절한 문제라고 생각이 들었습니다.
구역을 나눌 때 어렵게 생각하지 말고 for문에서 1번 구역이 x가 끝나는 end부분을 3번 구역 for문 x의 start 부분에 넣어 계산하는 노하우도 얻을 수있었습니다. 사실 당연한 것인데 저는 이게 맞나 계속 확인하면서 풀기 때문에 시간을 많이 뺏겼습니다. 아직 실력이 부족한 것 같고 감이 없는 것 같아서 더 노력해야 할 것 같습니다.
'ProblemSolving > 구현, 시뮬레이션, 완전탐색' 카테고리의 다른 글
| 백준 21610 마법사 상어와 비바라기 (파이썬) (0) | 2022.04.23 |
|---|---|
| 백준 20055 컨베이어 벨트 위의 로봇 (파이썬) (0) | 2022.04.19 |
| 백준 17140 이차원 배열과 연산 (Python) (0) | 2022.04.11 |
| 백준 14499 주사위 굴리기 (Python) (0) | 2022.04.06 |
| 백준 14500 테트로미노 - (Python) (0) | 2022.04.06 |